当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
2911:Digits on the Floor
题目描述
Taro attempts to tell digits to Hanako by putting straight bars on the floor. Taro wants to express each digit by making one of the forms shown in Figure 2.
Since Taro may not have bars of desired lengths, Taro cannot always make forms exactly as shown in Figure 2. Fortunately, Hanako can recognize a form as a digit if the connection relation between bars in the form is kept. Neither the lengths of bars nor the directions of forms affect Hanako抯 perception as long as the connection relation remains the same. For example, Hanako can recognize all the awkward forms in Figure 3 as digits. On the other hand, Hanako cannot recognize the forms in Figure 4 as digits. For clarity, touching bars are slightly separated in Figures 2, 3 and 4. Actually, touching bars overlap exactly at one single point.
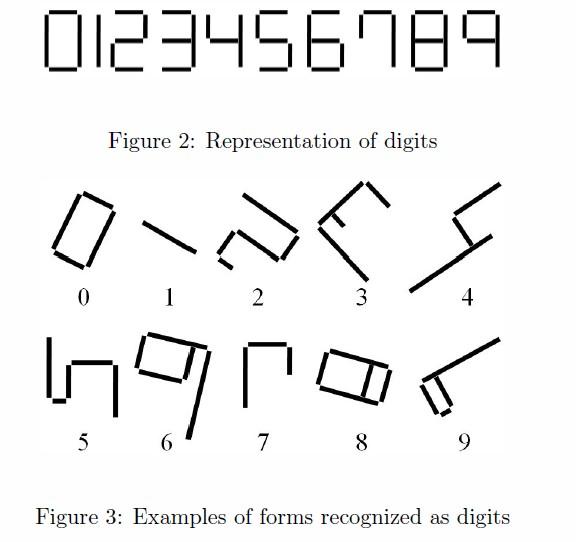
In the forms, when a bar touches another, the touching point is an end of at least one of them. That is, bars never cross. In addition, the angle of such two bars is always a right angle.
To enable Taro to represent forms with his limited set of bars, positions and lengths of bars can be changed as far as the connection relations are kept. Also, forms can be rotated. Keeping the connection relations means the following.
?Separated bars are not made to touch.
?Touching bars are not made separate.
?When one end of a bar touches another bar, that end still touches the same bar. When ittouches a midpoint of the other bar, it remains to touch a midpoint of the same bar on the same side.
?The angle of touching two bars is kept to be the same right angle (90 degrees and −90 degrees are considered different, and forms for 2 and 5 are kept distinguished). Your task is to find how many times each digit appears on the floor. The forms of some digits always contain the forms of other digits. For example, a form for 9 always contains four forms for 1, one form for 4, and two overlapping forms for 7. In this problem, ignore the forms contained in another form and count only the digit of the 搇argest?form composed of all mutually connecting bars. If there is one form for 9, it should be interpreted as one appearance of 9 and no appearance of 1, 4, or 7.
Since Taro may not have bars of desired lengths, Taro cannot always make forms exactly as shown in Figure 2. Fortunately, Hanako can recognize a form as a digit if the connection relation between bars in the form is kept. Neither the lengths of bars nor the directions of forms affect Hanako抯 perception as long as the connection relation remains the same. For example, Hanako can recognize all the awkward forms in Figure 3 as digits. On the other hand, Hanako cannot recognize the forms in Figure 4 as digits. For clarity, touching bars are slightly separated in Figures 2, 3 and 4. Actually, touching bars overlap exactly at one single point.

In the forms, when a bar touches another, the touching point is an end of at least one of them. That is, bars never cross. In addition, the angle of such two bars is always a right angle.
To enable Taro to represent forms with his limited set of bars, positions and lengths of bars can be changed as far as the connection relations are kept. Also, forms can be rotated. Keeping the connection relations means the following.
?Separated bars are not made to touch.
?Touching bars are not made separate.
?When one end of a bar touches another bar, that end still touches the same bar. When ittouches a midpoint of the other bar, it remains to touch a midpoint of the same bar on the same side.
?The angle of touching two bars is kept to be the same right angle (90 degrees and −90 degrees are considered different, and forms for 2 and 5 are kept distinguished). Your task is to find how many times each digit appears on the floor. The forms of some digits always contain the forms of other digits. For example, a form for 9 always contains four forms for 1, one form for 4, and two overlapping forms for 7. In this problem, ignore the forms contained in another form and count only the digit of the 搇argest?form composed of all mutually connecting bars. If there is one form for 9, it should be interpreted as one appearance of 9 and no appearance of 1, 4, or 7.
输入解释
The input consists of a number of datasets. Each dataset is formatted as follows.
n
x1a y1a x1b y1b
x2a y2a x2b y2b
...
xna yna xnb xnb
In the first line, n represents the number of bars in the dataset. For the rest of the lines, one line represents one bar. Four integers xa, ya, xb, yb, delimited by single spaces, are given in each line. xa and ya are the x- and y-coordinates of one end of the bar, respectively. xb and yb are those of the other end. The coordinate system is as shown in Figure 5. You can assume 1 ≤ n ≤ 1000 and 0 ≤ xa; ya; xb; yb ≤ 1000. The end of the input is indicated by a line containing one zero.

You can also assume the following conditions.
More than two bars do not overlap at one point.
Every bar is used as a part of a digit. Non-digit forms do not exist on the floor.
A bar that makes up one digit does not touch nor cross any bar that makes up another digit.
There is no bar whose length is zero.
n
x1a y1a x1b y1b
x2a y2a x2b y2b
...
xna yna xnb xnb
In the first line, n represents the number of bars in the dataset. For the rest of the lines, one line represents one bar. Four integers xa, ya, xb, yb, delimited by single spaces, are given in each line. xa and ya are the x- and y-coordinates of one end of the bar, respectively. xb and yb are those of the other end. The coordinate system is as shown in Figure 5. You can assume 1 ≤ n ≤ 1000 and 0 ≤ xa; ya; xb; yb ≤ 1000. The end of the input is indicated by a line containing one zero.

You can also assume the following conditions.
More than two bars do not overlap at one point.
Every bar is used as a part of a digit. Non-digit forms do not exist on the floor.
A bar that makes up one digit does not touch nor cross any bar that makes up another digit.
There is no bar whose length is zero.
输出解释
For each dataset, output a single line containing ten integers delimited by single spaces. These integers represent how many times 0, 1, 2, . . . , and 9 appear on the floor in this order.
Output lines must not contain other characters.
Output lines must not contain other characters.
输入样例
9 60 140 200 300 300 105 330 135 330 135 250 215 240 205 250 215 298 167 285 154 30 40 30 90 30 90 150 90 150 90 150 20 30 40 150 40 8 320 20 300 60 320 20 380 50 380 50 240 330 10 50 40 20 10 50 110 150 110 150 180 80 40 20 37 17 37 17 27 27 20 72 222 132 182 204 154 204 54 510 410 520 370 404 54 204 54 530 450 410 450 204 68 404 68 80 110 120 30 130 160 180 60 520 370 320 320 310 360 320 320 120 30 180 60 60 100 80 110 404 154 204 154 80 60 60 100 430 550 590 550 510 410 310 360 430 450 430 550 404 54 404 154 232 202 142 262 142 262 102 202 0
输出样例
0 1 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 1 0 0 1 0 1 0 2 0 0 0 1 0
来自杭电HDUOJ的附加信息
| Recommend | lcy |
最后修改于 2020-10-25T22:58:04+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 6000/2000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码