当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
2805:Aligning Two Shapes
题目描述
The knowledge about Shape from Wikipedia:
Simple two-dimensional shapes can be described by basic geometry such as points, line, curves, plane, and so on. (A shape whose points belong all the same plane is called a plane figure.) Most shapes occurring in the physical world are complex. Some, such as plant structures and coastlines, may be so arbitrary as to defy traditional mathematical description – in which case they may be analyzed by differential geometry, or as fractals.
Rigid shape definition
In geometry, two subsets of a Euclidean space have the same shape if one can be transformed to the other by a combination of translations, rotations (together also called rigid transformations), and uniform scalings. In other words, the shape of a set is all the geometrical information that is invariant to position (including rotation) and scale.
Having the same shape is an equivalence relation, and accordingly a precise mathematical definition of the notion of shape can be given as being an equivalence class of subsets of a Euclidean space having the same shape.
From the message above, we know that we can use the operations of translations, rotations and scaling to align two shapes.
Now we assume that the shapes we describe in the problem is form with a set of points. For example, a shape S = {x1, y1, x2, y2.... xn, yn}.
In the picture below, we use four points to represent a square. The two squares are all centred on the origin (0, 0). After the operation of scaling, S1 is coincides with S2.
To simplify the problem, we suppose two shapes, X1 and X2, centred on the origin (0, 0) initially. That means you can only use the operations of rotations and scaling, but not the translations. We wish to scale and rotate S1 by (s, θ) so as to minimize the sum of the square distances between the points of S1 and S2. Rotation means a two-dimensional object rotates around a center (or point).Scaling means a linear transformation that enlarges or diminishes objects.
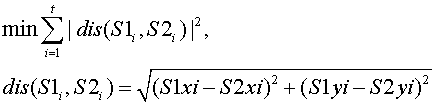
输入解释
Each test case contains a single integer t (t<=1000), indicating the size of the two shapes (i.e., each shape has t points). The next following t lines each contain two integers (xi, yi) representing the shape of S1, then following t lines stands for the shape of S2. The input is terminated by a set starting with t = 0.
输出解释
For each test case, you should output one line containing a real number representing the minimum distance of the two shapes after the operations of rotation and scaling. The number should be rounded to three fractional digits.
输入样例
4 1 1 1 -1 -1 1 -1 -1 2 2 2 -2 -2 2 -2 -2 0
输出样例
0.000
来自杭电HDUOJ的附加信息
| Recommend | lcy |
最后修改于 2020-10-25T22:56:59+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码