当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
2766:Equilibrium Mobile
题目描述

A mobile is a type of kinetic sculpture constructed to take advantage of the principle of equilibrium. It consists of a number of rods, from which weighted objects or further rods hang. The objects hanging from the rods balance each other, so that the rods remain more or less horizontal. Each rod hangs from only one string, which gives it freedom to rotate about the string.
We consider mobiles where each rod is attached to its string exactly in the middle, as in the figure underneath. You are given such a configuration, but the weights on the ends are chosen incorrectly, so that the mobile is not in equilibrium. Since that's not aesthetically pleasing, you decide to change some of the weights.
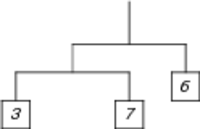
What is the minimum number of weights that you must change in order to bring the mobile to equilibrium? You may substitute any weight by any (possibly non-integer) weight. For the mobile shown in the figure, equilibrium can be reached by changing the middle weight from 7 to 3, so only 1 weight needs to changed.
输入解释
On the first line one positive number: the number of testcases, at most 100. After that per testcase:
* One line with the structure of the mobile, which is a recursively defined expression of the form:
<expr> ::= <weight> | "[" <expr> "," <expr> "]"
with <weight> a positive integer smaller than 109 indicating a weight and [<expr>,<expr>] indicating a rod with the two expressions at the ends of the rod. The total number of rods in the chain from a weight to the top of the mobile will be at most 16.
* One line with the structure of the mobile, which is a recursively defined expression of the form:
<expr> ::= <weight> | "[" <expr> "," <expr> "]"
with <weight> a positive integer smaller than 109 indicating a weight and [<expr>,<expr>] indicating a rod with the two expressions at the ends of the rod. The total number of rods in the chain from a weight to the top of the mobile will be at most 16.
输出解释
Per testcase:
* One line with the minimum number of weights that have to be changed.
* One line with the minimum number of weights that have to be changed.
输入样例
3 [[3,7],6] 40 [[2,3],[4,5]]
输出样例
1 0 3
来自杭电HDUOJ的附加信息
| Recommend | lcy |
最后修改于 2020-10-25T22:56:33+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码