当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
2763:The Two Note Rag
题目描述
Since most computers are binary machines, both powers of two and problems that involve only two values are important to computer scientists. The following problem has to do with powers of two and the digits 1 and 2.
Some powers of two as decimal values, such as 29 = 512 and 289 = 618,970,019,642,690,137,449,562,112 end in a string of digits consisting only of 1's and 2's (12 for 29 and 2112 for 289 ). In fact, it can be proved that:
For every integer R, there exists a power of 2 such that 2K uses only the digits 1 and 2 in its last R digits.
This is shown a bit more clearly in the following table:
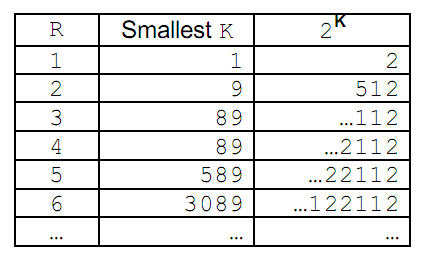
Your job is to write a program that will determine, for given R, the smallest K such that 2K ends in a string of R digits containing only 1's and 2's.
Some powers of two as decimal values, such as 29 = 512 and 289 = 618,970,019,642,690,137,449,562,112 end in a string of digits consisting only of 1's and 2's (12 for 29 and 2112 for 289 ). In fact, it can be proved that:
For every integer R, there exists a power of 2 such that 2K uses only the digits 1 and 2 in its last R digits.
This is shown a bit more clearly in the following table:

Your job is to write a program that will determine, for given R, the smallest K such that 2K ends in a string of R digits containing only 1's and 2's.
输入解释
The first line of the input contains a single decimal integer, N, 1 ≤ N ≤ 50, the number of problem data sets to follow. Each data set consists of a single integer R, 1 ≤ R ≤ 20, for which we want a power of 2 ending in a string of R 1's and 2's.
输出解释
For each data set, you should generate one line of output with the following values: The data set number as a decimal integer (start counting at one), a space, the input value R, another space, and the smallest value K for which 2K ends in a string of R 1's and 2's.
输入样例
6 1 2 4 5 7 15
输出样例
1 1 1 2 2 9 3 4 89 4 5 589 5 7 3089 6 15 11687815589
来自杭电HDUOJ的附加信息
| Recommend | lcy |
最后修改于 2020-10-25T22:56:31+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码