当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
2706:Line & Circle Maze
题目描述
A deranged algorithms professor has devised a terrible final exam: he throws his students into a strange maze formed entirely of linear and circular paths, with line segment endpoints and object intersections forming the junctions of the maze. The professor gives his students a map of the maze and a fixed amount of time to find the exit before he floods the maze with xerobiton particles, causing anyone still in the maze to be immediately inverted at the quantum level. Students who escape pass the course; those who don't are trapped forever in a parallel universe where the grass is blue and the sky is green.
The entrance and the exit are always at a junction as defined above. Knowing that clever ACM programming students will always follow the shortest possible path between two junctions, he chooses the entrance and exit junctions so that the distance that they have to travel is as far as possible. That is, he examines all pairs of junctions that have a path between them, and selects a pair of junctions whose shortest path distance is the longest possible for the maze (which he rebuilds every semester, of course, as the motivation to cheat on this exam is very high).
The joy he derives from quantumly inverting the majority of his students is marred by the tedium of computing the length of the longest of the shortest paths (he needs this to know to decide how much time to put on the clock), so he wants you to write a program to do it for him. He already has a program that generates the mazes, essentially just a random collection of line segments and circles. Your job is to take that collection of line segments and circles, determine the shortest paths between all the distinct pairs of junctions, and report the length of the longest one.
The input to your program is the output of the program that generates his mazes. That program was written by another student, much like yourself, and it meets a few of the professor's specifications:
1) No endpoint of a line segment will lie on a circle;
2)No line segment will intersect a circle at a tangent;
3) If two circles intersect, they intersect at exactly two distinct points;
4)Every maze contains at least two junctions; that is, a minimum maze is either a single line segment, or two circles that intersect.
There is, however, one bug in the program. (He would like to have it fixed, but unfortunately the student who wrote the code never gave him the source, and is now forever trapped in a parallel universe.) That bug is that the maze is not always entirely connected. There might be line segments or circles, or both, off by themselves that intersect nothing, or even little "submazes" composed of intersecting line segments and circles that as a whole are not connected to the rest of the maze. The professor insists that your solution account for this! The length that you report must be for a path between connected junctions!
Example:
1. 2.
2.
3. 4.
4.
Detail Description:
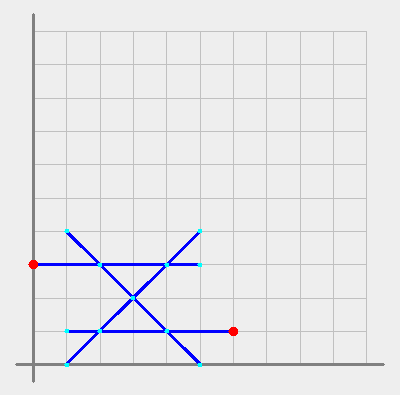
Pictrue 1: Line segments only. The large dots are the junction pair
whose shortest path is the longest possible.
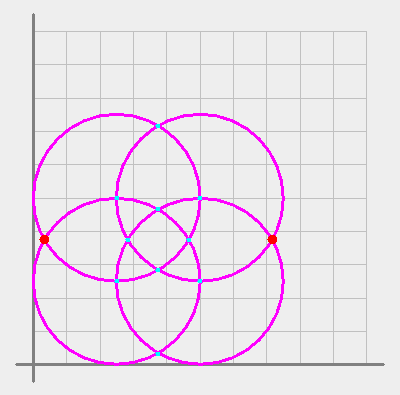
Pictrue 2: An example using circles only. Note that in this case there is
also another pair of junctions with the same length longest
possible shortest path.
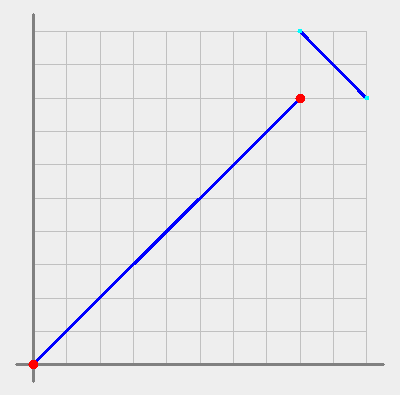
Pictrue 3: Disconnected components.
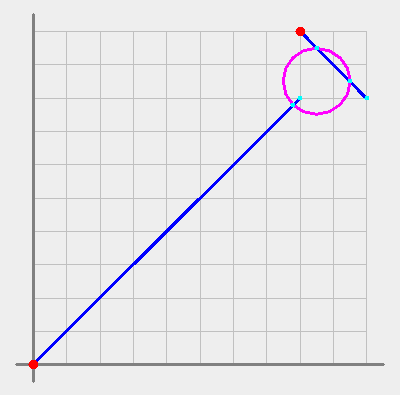
Pictrue 4: Now the line segments are connected by a circle, allowing for
a longer shortest path.
The entrance and the exit are always at a junction as defined above. Knowing that clever ACM programming students will always follow the shortest possible path between two junctions, he chooses the entrance and exit junctions so that the distance that they have to travel is as far as possible. That is, he examines all pairs of junctions that have a path between them, and selects a pair of junctions whose shortest path distance is the longest possible for the maze (which he rebuilds every semester, of course, as the motivation to cheat on this exam is very high).
The joy he derives from quantumly inverting the majority of his students is marred by the tedium of computing the length of the longest of the shortest paths (he needs this to know to decide how much time to put on the clock), so he wants you to write a program to do it for him. He already has a program that generates the mazes, essentially just a random collection of line segments and circles. Your job is to take that collection of line segments and circles, determine the shortest paths between all the distinct pairs of junctions, and report the length of the longest one.
The input to your program is the output of the program that generates his mazes. That program was written by another student, much like yourself, and it meets a few of the professor's specifications:
1) No endpoint of a line segment will lie on a circle;
2)No line segment will intersect a circle at a tangent;
3) If two circles intersect, they intersect at exactly two distinct points;
4)Every maze contains at least two junctions; that is, a minimum maze is either a single line segment, or two circles that intersect.
There is, however, one bug in the program. (He would like to have it fixed, but unfortunately the student who wrote the code never gave him the source, and is now forever trapped in a parallel universe.) That bug is that the maze is not always entirely connected. There might be line segments or circles, or both, off by themselves that intersect nothing, or even little "submazes" composed of intersecting line segments and circles that as a whole are not connected to the rest of the maze. The professor insists that your solution account for this! The length that you report must be for a path between connected junctions!
Example:
1.
 2.
2.
3.
 4.
4.
Detail Description:
Pictrue 1: Line segments only. The large dots are the junction pair
whose shortest path is the longest possible.
Pictrue 2: An example using circles only. Note that in this case there is
also another pair of junctions with the same length longest
possible shortest path.
Pictrue 3: Disconnected components.
Pictrue 4: Now the line segments are connected by a circle, allowing for
a longer shortest path.
输入解释
An input test case is a collection of line segments and circles. A line segment is specified as "L X1 Y1 X2 Y2" where "L" is a literal character, and (X1,Y1) and (X2,Y2) are the line segment endpoints. A circle is specified by "C X Y R" where "C" is a literal character, (X,Y) is the center of the circle, and R is its radius. All input values are integers, and line segment and circle objects are entirely contained in the first quadrant within the box defined by (0,0) at the lower left and (100,100) at the upper right. Each test case will consist of from 1 to 20 objects, terminated by a line containing only a single asterisk. Following the final test case, a line containing only a single asterisk marks the end of the input.
输出解释
For each input maze, output "Case N: ", where N is the input case number starting at one (1), followed by the length, rounded to one decimal, of the longest possible shortest path between a pair of connected junctions.
输入样例
L 10 0 50 40 L 10 4 0 50 0 L 10 1 0 60 1 0 L 0 30 50 30 * C 25 2 5 25 C 50 2 5 25 C 25 5 0 25 C 50 5 0 25 * L 0 0 80 80 L 80 1 00 100 80 * L 0 0 80 80 L 80 1 00 100 80 C 85 8 5 10 * *
输出样例
Ca se 1: 68.3 Ca se 2: 78.5 Ca se 3: 113.1 Ca se 4: 140.8
来自杭电HDUOJ的附加信息
| Recommend | zty |
最后修改于 2020-10-25T22:56:06+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码