当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
2704:Bulletin Board
题目描述
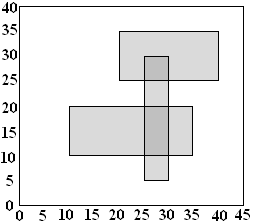
The ACM Student Chapter has just been given custody of a number of school bulletin boards. Several members agreed to clear off the old posters. They found posters plastered many levels deep. They made a bet about how much area was left clear, what was the greatest depth of posters on top of each other, and how much of the area was covered to this greatest depth. To determine each bet's winner, they made very accurate measurements of all the poster positions as they removed them. Because of the large number of posters, they now need a program to do the calculations. That is your job.
A simple illustration is shown above: a bulletin board 45 units wide by 40 high, with three posters, one with corners at coordinates (10, 10) and (35, 20), another with corners at (20, 25) and (40, 35), and the last with
corners at (25, 5) and (30, 30). The total area not covered by any poster is 1300. The maximum number of posters on top of each other is 2. The total area covered by exactly 2 posters is 75.
输入解释
The input will consist of one to twenty data sets, followed by a line containing only 0. On each line the data will consist of blank separated nonnegative integers.
The first line of a dataset contains integers n w h, where n is the number of posters on the bulletin board, w and h are the width and height of the bulletin board. Constraints are 0 < n <= 100; 0 < w <= 50000; 0 < h <= 40000.
The dataset ends with n lines, each describing the location of one poster. Each poster is rectangular and has horizontal and vertical sides. The x and y coordinates are measured from one corner of the bulletin board. Each line contains four numbers xl yl xh and yh, where xl and yl, are the lowest values of the x and y coordinates in one corner of the poster and xh and yh are the highest values in the diagonally opposite corner.Each poster fits on the bulletin board, so 0 2 xl < xh 2 w, and 0 2 yl < yh 2 h.
The first line of a dataset contains integers n w h, where n is the number of posters on the bulletin board, w and h are the width and height of the bulletin board. Constraints are 0 < n <= 100; 0 < w <= 50000; 0 < h <= 40000.
The dataset ends with n lines, each describing the location of one poster. Each poster is rectangular and has horizontal and vertical sides. The x and y coordinates are measured from one corner of the bulletin board. Each line contains four numbers xl yl xh and yh, where xl and yl, are the lowest values of the x and y coordinates in one corner of the poster and xh and yh are the highest values in the diagonally opposite corner.Each poster fits on the bulletin board, so 0 2 xl < xh 2 w, and 0 2 yl < yh 2 h.
输出解释
There is one line of output for each data set containing three integers, the total area of the bulletin board that is not covered by any poster, the maximum depth of posters on top of each other, and the total area covered this maximum number of times.
Caution: An approach examining every pair of integer coordinates might need to deal with 2 billion coordinate pairs.
Caution: An approach examining every pair of integer coordinates might need to deal with 2 billion coordinate pairs.
输入样例
3 45 40 10 10 35 20 20 25 40 35 25 5 30 30 1 20 30 5 5 15 25 2 2000 1000 0 0 1000 1000 1000 0 2000 1000 3 10 10 0 0 10 10 0 0 10 10 0 0 10 10 0
输出样例
1300 2 75 400 1 200 0 1 2000000 0 3 100
来自杭电HDUOJ的附加信息
| Recommend | zty |
最后修改于 2020-10-25T22:56:05+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码