当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
2683:TCE-frep number system
题目描述
Number theory is one of the oldest branches of pure mathematics, and one of the largest. Of course, it concerns questions about numbers, usually meaning whole numbers or rational numbers (fractions).
Elementary number theory involves divisibility among integers -- the division "algorithm", the Euclidean algorithm (and thus the existence of greatest common divisors), elementary properties of primes (the unique factorization theorem, the infinitude of primes), congruences, including Fermat's little theorem and Euler's theorem extending it. But the term "elementary" is usually used in this setting only to mean that no advanced tools from other areas are used -- not that the results themselves are simple.
Topics in elementary number theory -- the solutions of sets of linear congruence equations (the Chinese Remainder Theorem), or solutions of single binary quadratic equations (Pell's equations and continued fractions), or the generation of Fibonacci numbers or Pythagorean triples -- turn out in retrospect to be harbingers of sophisticated tools and themes in other areas. The remaining parts of number theory are more or less closely allied with other branches of mathematics, and typically use tools from those areas.
Also there lots of branches, such as Combinatorial Number Theory, Algebraic Number Theory, Analytic Number Theory, additive number theory, Geometric number theory, Transcendental number theory, etc.
Today give you a function g(n) whose value is the sum of all the divisors of n .
If n satisfies following rule:
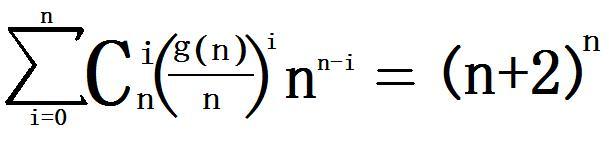
We call n is a TCE-frep number,your task is easy,detail to input and output.
Elementary number theory involves divisibility among integers -- the division "algorithm", the Euclidean algorithm (and thus the existence of greatest common divisors), elementary properties of primes (the unique factorization theorem, the infinitude of primes), congruences, including Fermat's little theorem and Euler's theorem extending it. But the term "elementary" is usually used in this setting only to mean that no advanced tools from other areas are used -- not that the results themselves are simple.
Topics in elementary number theory -- the solutions of sets of linear congruence equations (the Chinese Remainder Theorem), or solutions of single binary quadratic equations (Pell's equations and continued fractions), or the generation of Fibonacci numbers or Pythagorean triples -- turn out in retrospect to be harbingers of sophisticated tools and themes in other areas. The remaining parts of number theory are more or less closely allied with other branches of mathematics, and typically use tools from those areas.
Also there lots of branches, such as Combinatorial Number Theory, Algebraic Number Theory, Analytic Number Theory, additive number theory, Geometric number theory, Transcendental number theory, etc.
Today give you a function g(n) whose value is the sum of all the divisors of n .
If n satisfies following rule:
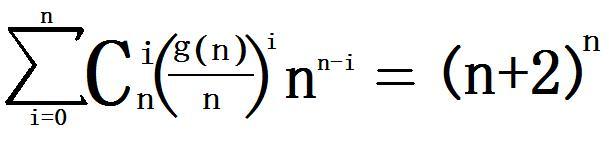
We call n is a TCE-frep number,your task is easy,detail to input and output.
输入解释
Two ways of input:
A x y
(x, y <= 2^63-1)
Q n
(1 <= n <= 2^63-1)
A x y
(x, y <= 2^63-1)
Q n
(1 <= n <= 2^63-1)
输出解释
For A x y , output the number of TCE-frep number which located between x and y
For Q n , output “1” if n is a TCE-frep number else output “0”
For Q n , output “1” if n is a TCE-frep number else output “0”
输入样例
A 5 70 A 6 6 Q 6 Q 1
输出样例
2 1 1 0
来自杭电HDUOJ的附加信息
| Author | WhereIsHeroFrom |
| Recommend | lcy |
最后修改于 2020-10-25T22:55:53+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码