当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
2558:Cutting trees
题目描述
A rooted graph is an indirected graph with every edge attached by some path to a special vertex called the root or the ground. The ground is denoted in the below figures that follow by a dotted line.
A bamboo stalk with n segments is a linear graph of n edges with the bottom of the n edges rooted to the ground. A move consists of hacking away one of the segments, and removing that segment and all segments above it no longer connectd to the ground. Two players alternate moves and the last player to move wins. A single bamboo stalk of n segments can be moved into a bamboo stalk of any smaller number of segments from n-1 to 0. So a single bamboo stalk of n segments is equivalent to a nim pile of n chips.
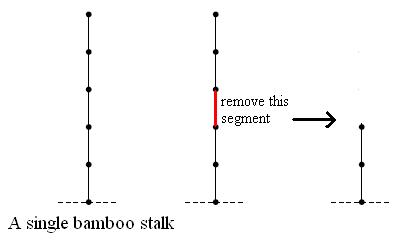
As you known, the player who moves first can win the the game with only one bamboo stalk. So many people always play the game with several bamboo stalks. One example is as below:
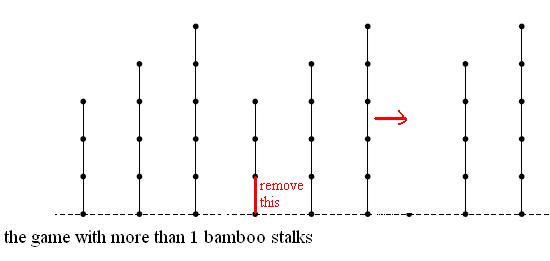
Playing a sum of games of bamboo stalks is thus equivalent to playing a nim game that with several piles. A move consisits of selecting a bamboo stalk containg n segments and hacking away one of the segments in the selected bamboo stalk.
I think the nim game is easy for you, the smart ACMers. So, today, we play a game named "cutting trees". A "rooted tree" is a graph with a distinguished vertex called the root, with the property that from every vertex there is unique path(that doesn't repeat edges) to the root. Essentially this means there are no cycles.
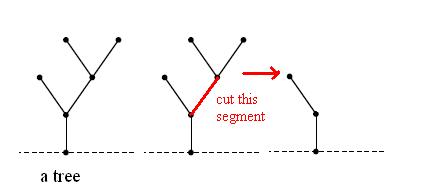
Of course, in the game "cutting trees", there are several trees.Again, a move consisits of selecting a tree and hacking away any segment and removing segment and anything not connected to the ground. The player who cuts the last segment wins the game.
A bamboo stalk with n segments is a linear graph of n edges with the bottom of the n edges rooted to the ground. A move consists of hacking away one of the segments, and removing that segment and all segments above it no longer connectd to the ground. Two players alternate moves and the last player to move wins. A single bamboo stalk of n segments can be moved into a bamboo stalk of any smaller number of segments from n-1 to 0. So a single bamboo stalk of n segments is equivalent to a nim pile of n chips.

As you known, the player who moves first can win the the game with only one bamboo stalk. So many people always play the game with several bamboo stalks. One example is as below:

Playing a sum of games of bamboo stalks is thus equivalent to playing a nim game that with several piles. A move consisits of selecting a bamboo stalk containg n segments and hacking away one of the segments in the selected bamboo stalk.
I think the nim game is easy for you, the smart ACMers. So, today, we play a game named "cutting trees". A "rooted tree" is a graph with a distinguished vertex called the root, with the property that from every vertex there is unique path(that doesn't repeat edges) to the root. Essentially this means there are no cycles.

Of course, in the game "cutting trees", there are several trees.Again, a move consisits of selecting a tree and hacking away any segment and removing segment and anything not connected to the ground. The player who cuts the last segment wins the game.
输入解释
Standard input will contain multiple test cases. The first line of the input is a single integer T which is the number of test cases. T test cases follow.
Each case begins with a N(1<=N<=1000), the number of trees in the game.A tree is decribed by a number m, the nodes of the tree and R(0<=R<=m-1), the root of the tree. Then m-1 lines follow, each line containg two positive integers A,B∈[0,m-1], means that there is a edge between A and B.
In the game, the first player always moves first.
Each case begins with a N(1<=N<=1000), the number of trees in the game.A tree is decribed by a number m, the nodes of the tree and R(0<=R<=m-1), the root of the tree. Then m-1 lines follow, each line containg two positive integers A,B∈[0,m-1], means that there is a edge between A and B.
In the game, the first player always moves first.
输出解释
Results should be directed to standard output. For each case, if the first player wins, ouput "The first player wins", or else, output "The second player wins",in a single line.
输入样例
1 1 4 0 0 1 1 2 1 3
输出样例
The first player wins
来自杭电HDUOJ的附加信息
| Recommend | lcy |
最后修改于 2020-10-25T22:54:37+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 5000/1000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码