当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
2417:Kadj Squares
题目描述
In this problem, you are given a sequence S1, S2, ..., Sn of squares of different sizes. The sides of the squares are integer numbers. We locate the squares on the positive x-y quarter of the plane, such that their sides make 45 degrees with x and y axes, and one of their vertices are on y=0 line. Let bi be the x coordinates of the bottom vertex of Si. First, put S1 such that its left vertex lies on x=0. Then, put S1, (i > 1) at minimum bi such that
bi > bi-1 and
the interior of Si does not have intersection with the interior of S1...Si-1.
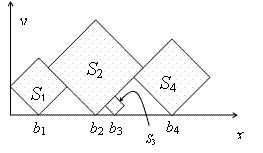
The goal is to find which squares are visible, either entirely or partially, when viewed from above. In the example above, the squares S1, S2, and S4 have this property. More formally, Si is visible from above if it contains a point p, such that no square other than Si intersect the vertical half-line drawn from p upwards.
bi > bi-1 and
the interior of Si does not have intersection with the interior of S1...Si-1.

The goal is to find which squares are visible, either entirely or partially, when viewed from above. In the example above, the squares S1, S2, and S4 have this property. More formally, Si is visible from above if it contains a point p, such that no square other than Si intersect the vertical half-line drawn from p upwards.
输入解释
The input consists of multiple test cases. The first line of each test case is n (1 ≤ n ≤ 50), the number of squares. The second line contains n integers between 1 to 30, where the ith number is the length of the sides of Si. The input is terminated by a line containing a zero number.
输出解释
For each test case, output a single line containing the index of the visible squares in the input sequence, in ascending order, separated by blank characters.
输入样例
4 3 5 1 4 3 2 1 2 0
输出样例
1 2 4 1 3
来自杭电HDUOJ的附加信息
| Recommend | lcy |
最后修改于 2020-10-25T22:53:16+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码