当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
1844:Intermediate Rounds for Multicasting
题目描述
Consider a communication network consisting of N nodes numbered from 1 to N. The nodes are interconnected in such a way that the network has the shape of a rooted tree, with node 1 as the root. Node 1 wants to send a message (the same message) to each node which is a leaf in the tree (i.e. has no sons) – this operation is known as multicast. A message can only be sent from one node to one of its descendants (including the node itself). Each edge of the tree has an associated cost and the cost of sending a message from a node X to one of its descendants Y is the sum of the costs of the edges on the unique path from X to Y (if X=Y, then the cost is 0). The total cost of a multicast strategy is the sum of the costs of sending each message.
In order to reach its goal, node 1 will use the following multicast strategy: The strategy consists of K intermediate rounds. In the first round, node 1 sends an individual message to a subset of nodes S1 such that each leaf is a descendant of exactly one node X in S1 (this means that any node X in S1 is not a descendant of another node Y in S1). In round i (2<=i<=K), each node X in Si-1 sends an individual message to a subset Si,X of nodes from its subtree, such that each leaf which is a descendant of X is also a descendant of exactly one node in Si,X. The set of nodes Si is the union of the sets Si,X, for each X in Si-1. In the end, each node X in Sk must send a message to each leaf node which is a descendant of X.
Given the communication network, the cost of each edge and the number of intermediate rounds K, find the minimum total cost of a multicast strategy.
In order to reach its goal, node 1 will use the following multicast strategy: The strategy consists of K intermediate rounds. In the first round, node 1 sends an individual message to a subset of nodes S1 such that each leaf is a descendant of exactly one node X in S1 (this means that any node X in S1 is not a descendant of another node Y in S1). In round i (2<=i<=K), each node X in Si-1 sends an individual message to a subset Si,X of nodes from its subtree, such that each leaf which is a descendant of X is also a descendant of exactly one node in Si,X. The set of nodes Si is the union of the sets Si,X, for each X in Si-1. In the end, each node X in Sk must send a message to each leaf node which is a descendant of X.
Given the communication network, the cost of each edge and the number of intermediate rounds K, find the minimum total cost of a multicast strategy.
输入解释
The first line of input contains an integer number T, representing the number of test cases to follow. The first line of each test case contains 2 integer numbers: N (1<=N<=333) and K (1<=K<=10). The next N-1 lines contain 3 integers each: A, B and C (1<=C<=10.000), meaning that node B is a son of node A and the edge (A,B) has cost C.
输出解释
For each of the T test cases, in the order given in the input, print one line containing the minimum total cost of a multicast strategy having the specified properties.
输入样例
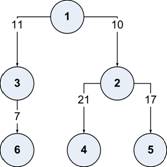
1 6 1 1 2 10 1 3 11 2 4 21 2 5 17 3 6 7
输出样例
66
提示
In the first (and only) intermediate round, node 1 sends messages to node 6 (with cost 18) and to node 2 (with cost 10).
So the set S1 is {2,6}. In the end, node 6 will send a message to itself (with cost 0) and node 2 will send messages to node 4 (with cost 21)
and to node 5 (with cost 17). The total cost is 18+10+21+17=66.
来自杭电HDUOJ的附加信息
| Author | Mugurel Ionut Andreica |
| Recommend | lcy |
最后修改于 2020-10-25T22:48:14+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 1000/1000MS(Java/Others) | 65535/65535K(Java/Others) |
登陆或注册以提交代码