当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
1793:Minimal search cost
题目描述
As we know, we need to spend O(n) time in the abstract finding a key(every two keys are different) in a non-sorted array. But if we make up a BST(binary search tree) before, then for each access, you need to spend log(N) time to do it. And for each access, there exists a road from the root node to the target node, whose length Ci is the number of the edges of the road.
Because there is an accessing frequency Fi for each key. And the total value of the tree is defined as following rule: SUM=Sigma(Ci*Fi), for i from 0 to N-1, N is the number of the keys. You need to find the minimal value M_SUM to make up a tree.
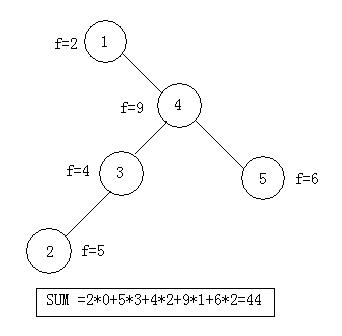
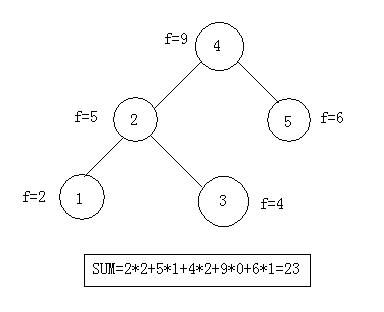
Because there is an accessing frequency Fi for each key. And the total value of the tree is defined as following rule: SUM=Sigma(Ci*Fi), for i from 0 to N-1, N is the number of the keys. You need to find the minimal value M_SUM to make up a tree.


输入解释
There are a lot of cases. In each case, in the first line, there is an integer N to represent the number of keys. In the second line, there are N sorted integers Ki. In the third line, there are N integers Fi, which are the accessing frequency. 0<N<=1000, 0<=Fi<65536.
输出解释
For each case, just output the minimal search cost.
输入样例
5 1 2 3 4 5 2 5 4 9 6
输出样例
23
来自杭电HDUOJ的附加信息
| Author | wangye |
| Recommend | wangye |
最后修改于 2020-10-25T22:47:48+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 10000/4000MS(Java/Others) | 65536/32768K(Java/Others) |
登陆或注册以提交代码