当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
1694:Final Challenge
题目描述
Definite integral is an important part of Mathematical Analysis. During Mathematical Analysis lessons, students always find it quite hard to calculate the definite integral. And the software Mathematic is so complex that very few students can master its usage.
So can you develop a simple tool to help the students calculate the definite integral? It’s the final challenge in this contest. This task requires many skills and is so challenging that probably only the god can solve it in 5 hours. Can you solve it and become a god-like person?
Next is the format for all functions in this challenge:
There are six types of basic elementary function:
1、 constant function: C;
2、 power function: x^C;
3、 exponential function: e^x;
4、 logarithmic function: ln(x);
5、 trigonometric function: sin(x), cos(x), tan(x), cot(x), sec(x), cot(x);
6、 inverse circular trigonometric function: asin(x), acos(x), atan(x).
C is a constant number between -100 and 100.
Elementary function is basic elementary function and their composite functions. There are ten types of composite functions. (A and B represent elementary functions)
1、 A+B;
2、 A-B;
3、 -A;
4、 A*B;
5、 A/B;
6、 A^B;
7、 e^A;
8、 ln(A);
9、 sin(A), cos(A), tan(A), cot(A), sec(A), csc(A);
10、 asin(A), acos(A), atan(A).
Arithmetic priority: () > ^ > *, / > +,-
In this problem, the task can be proper integral, improper integral; it is also possible that its indefinite integral isn’t even an elementary function. But you can assume that, if the integrating range is [a,b], then (a,b) will be a subset of the function’s definitions. You can also assume that for any improper integral, the result of it will converge. Finally, it is guaranteed that the final result is between -10,000 and 10,000.
So can you develop a simple tool to help the students calculate the definite integral? It’s the final challenge in this contest. This task requires many skills and is so challenging that probably only the god can solve it in 5 hours. Can you solve it and become a god-like person?
Next is the format for all functions in this challenge:
There are six types of basic elementary function:
1、 constant function: C;
2、 power function: x^C;
3、 exponential function: e^x;
4、 logarithmic function: ln(x);
5、 trigonometric function: sin(x), cos(x), tan(x), cot(x), sec(x), cot(x);
6、 inverse circular trigonometric function: asin(x), acos(x), atan(x).
C is a constant number between -100 and 100.
Elementary function is basic elementary function and their composite functions. There are ten types of composite functions. (A and B represent elementary functions)
1、 A+B;
2、 A-B;
3、 -A;
4、 A*B;
5、 A/B;
6、 A^B;
7、 e^A;
8、 ln(A);
9、 sin(A), cos(A), tan(A), cot(A), sec(A), csc(A);
10、 asin(A), acos(A), atan(A).
Arithmetic priority: () > ^ > *, / > +,-
In this problem, the task can be proper integral, improper integral; it is also possible that its indefinite integral isn’t even an elementary function. But you can assume that, if the integrating range is [a,b], then (a,b) will be a subset of the function’s definitions. You can also assume that for any improper integral, the result of it will converge. Finally, it is guaranteed that the final result is between -10,000 and 10,000.
输入解释
The input consists of several test cases. There is a single number above all, the number of cases. There are no more than 50 cases.
Each case contains two lines. The first line contains the function f(x) in the format above. There are no more than 300 letters each. There aren’t any whitespaces in the function.
The second line contains two floating numbers, a and b, -10,100 <= a, b <= 10,000 representing the integrating range. Notice that a and b can also be INF, -INF representing ∞ and -∞.
Each case contains two lines. The first line contains the function f(x) in the format above. There are no more than 300 letters each. There aren’t any whitespaces in the function.
The second line contains two floating numbers, a and b, -10,100 <= a, b <= 10,000 representing the integrating range. Notice that a and b can also be INF, -INF representing ∞ and -∞.
输出解释
For each case, print the value of 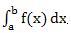 . The answer should be rounded to six digits to the right of the decimal point. Use the format in the sample.
. The answer should be rounded to six digits to the right of the decimal point. Use the format in the sample.
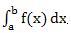 . The answer should be rounded to six digits to the right of the decimal point. Use the format in the sample.
. The answer should be rounded to six digits to the right of the decimal point. Use the format in the sample.输入样例
3 x 1 2 sin(x)^2/(sin(x)+cos(x)) 0 1.5707963268 e^(-x) 0 INF
输出样例
Case 1: 1.500000 Case 2: 0.623225 Case 3: 1.000000
来自杭电HDUOJ的附加信息
| Recommend | wangye |
最后修改于 2020-10-25T22:47:16+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 10000/5000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码