当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
1687:Lucky Light
题目描述
We have a (point) light source at position (xL, yL) with yL > 0, and a finite series of line segments, all of finite non-zero length, given by the coordinates of their two endpoints. These endpoints are all different. The line segments are all situated above the x-axis (y > 0).
The segments cast their shadows onto the x-axis. We assume that the shadows of two segments either do not overlap at all, or have an overlap that has some non-zero width (they do not just touch). We also assume that for each segment its shadow is more than just one point, i.e., there is no segment that is directed toward the light source. The height of the light source (yL) is at least 1 unit larger than the y-coordinates of the endpoints of the line segments. This guarantees that indeed each line segment has a bounded shadow on the x-axis.
The collection of shadows divides the x-axis into dark and lighted areas (intervals). The problem is to determine the number of lighted areas — which is at least 2 (if there is at least one line segment, otherwise it is 1).
In the picture below the three line segments A, B and C cause three lighted areas, as indicated.
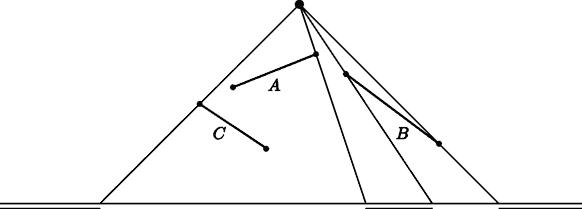
The segments cast their shadows onto the x-axis. We assume that the shadows of two segments either do not overlap at all, or have an overlap that has some non-zero width (they do not just touch). We also assume that for each segment its shadow is more than just one point, i.e., there is no segment that is directed toward the light source. The height of the light source (yL) is at least 1 unit larger than the y-coordinates of the endpoints of the line segments. This guarantees that indeed each line segment has a bounded shadow on the x-axis.
The collection of shadows divides the x-axis into dark and lighted areas (intervals). The problem is to determine the number of lighted areas — which is at least 2 (if there is at least one line segment, otherwise it is 1).
In the picture below the three line segments A, B and C cause three lighted areas, as indicated.

输入解释
The first line of the input file contains a single number: the number of test cases to follow. Each test case has the following format:
One line with one integer n with 0 ≤ n ≤ 100: the number of line segments.
One line with two integers xL and yL, the coordinates of the light source, separated by a single space. The coordinates satisfy -100 ≤ xL ≤ 100 and 1 ≤ yL ≤ 1,000.
n lines, each containing four integers xi, yi, ui and vi, separated by single spaces, that specify x- and y-coordinates of the two endpoints (xi, yi) and (ui, vi) of the ith line segment, where -100 ≤ xi, ui ≤ 100 and 0 < yi, vi < yL, for 1 ≤ i ≤ n.
One line with one integer n with 0 ≤ n ≤ 100: the number of line segments.
One line with two integers xL and yL, the coordinates of the light source, separated by a single space. The coordinates satisfy -100 ≤ xL ≤ 100 and 1 ≤ yL ≤ 1,000.
n lines, each containing four integers xi, yi, ui and vi, separated by single spaces, that specify x- and y-coordinates of the two endpoints (xi, yi) and (ui, vi) of the ith line segment, where -100 ≤ xi, ui ≤ 100 and 0 < yi, vi < yL, for 1 ≤ i ≤ n.
输出解释
For every test case in the input file, the output should contain a single number, on a single line: the number of lighted areas.
输入样例
2 3 50 60 55 45 30 35 64 39 92 18 20 30 40 16 2 -10 50 -10 1 10 11 -10 11 10 1
输出样例
3 2
来自杭电HDUOJ的附加信息
| Recommend | lcy |
最后修改于 2020-10-25T22:47:11+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 3000/1000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码