当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
1619:Unidirectional TSP
题目描述
Problems that require minimum paths through some domain appear in many different areas of computer science. For example, one of the constraints in VLSI routing problems is minimizing wire length. The Traveling Salesperson Problem (TSP) -- finding whether all the cities in a salesperson's route can be visited exactly once with a specified limit on travel time -- is one of the canonical examples of an NP-complete problem; solutions appear to require an inordinate amount of time to generate, but are simple to check.
This problem deals with finding a minimal path through a grid of points while traveling only from left to right.
Given an m*n matrix of integers, you are to write a program that computes a path of minimal weight. A path starts anywhere in column 1 (the first column) and consists of a sequence of steps terminating in column n (the last column). A step consists of traveling from column i to column i+1 in an adjacent (horizontal or diagonal) row. The first and last rows (rows 1 and m) of a matrix are considered adjacent, i.e., the matrix ``wraps'' so that it represents a horizontal cylinder. Legal steps are illustrated below.
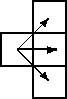
The weight of a path is the sum of the integers in each of the n cells of the matrix that are visited.
For example, two slightly different 5*6 matrices are shown below (the only difference is the numbers in the bottom row).
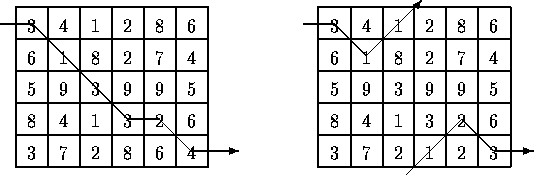
The minimal path is illustrated for each matrix. Note that the path for the matrix on the right takes advantage of the adjacency property of the first and last rows.
This problem deals with finding a minimal path through a grid of points while traveling only from left to right.
Given an m*n matrix of integers, you are to write a program that computes a path of minimal weight. A path starts anywhere in column 1 (the first column) and consists of a sequence of steps terminating in column n (the last column). A step consists of traveling from column i to column i+1 in an adjacent (horizontal or diagonal) row. The first and last rows (rows 1 and m) of a matrix are considered adjacent, i.e., the matrix ``wraps'' so that it represents a horizontal cylinder. Legal steps are illustrated below.

The weight of a path is the sum of the integers in each of the n cells of the matrix that are visited.
For example, two slightly different 5*6 matrices are shown below (the only difference is the numbers in the bottom row).

The minimal path is illustrated for each matrix. Note that the path for the matrix on the right takes advantage of the adjacency property of the first and last rows.
输入解释
The input consists of a sequence of matrix specifications. Each matrix specification consists of the row and column dimensions in that order on a line followed by integers where m is the row dimension and n is the column dimension. The integers appear in the input in row major order, i.e., the first n integers constitute the first row of the matrix, the second n integers constitute the second row and so on. The integers on a line will be separated from other integers by one or more spaces. Note: integers are not restricted to being positive. There will be one or more matrix specifications in an input file. Input is terminated by end-of-file.
For each specification the number of rows will be between 1 and 10 inclusive; the number of columns will be between 1 and 100 inclusive. No path's weight will exceed integer values representable using 30 bits
For each specification the number of rows will be between 1 and 10 inclusive; the number of columns will be between 1 and 100 inclusive. No path's weight will exceed integer values representable using 30 bits
输出解释
Two lines should be output for each matrix specification in the input file, the first line represents a minimal-weight path, and the second line is the cost of a minimal path. The path consists of a sequence of n integers (separated by one or more spaces) representing the rows that constitute the minimal path. If there is more than one path of minimal weight the path that is lexicographically smallest should be output.
输入样例
5 6 3 4 1 2 8 6 6 1 8 2 7 4 5 9 3 9 9 5 8 4 1 3 2 6 3 7 2 8 6 4 5 6 3 4 1 2 8 6 6 1 8 2 7 4 5 9 3 9 9 5 8 4 1 3 2 6 3 7 2 1 2 3 2 2 9 10 9 10
输出样例
1 2 3 4 4 5 16 1 2 1 5 4 5 11 1 1 19
来自杭电HDUOJ的附加信息
| Recommend | 8600 |
最后修改于 2020-10-25T22:46:32+00:00 由爬虫自动更新
共提交 45 次
通过率 13.33%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 65536/32768K(Java/Others) |
登陆或注册以提交代码