当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
1615:Fermat vs. Pythagoras
题目描述
Computer generated and assisted proofs and verification occupy a small niche in the realm of Computer Science. The first proof of the four-color problem was completed with the assistance of a computer program and current efforts in verification have succeeded in verifying the translation of high-level code down to the chip level.
This problem deals with computing quantities relating to part of Fermat's Last Theorem: that there are no integer solutions of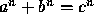 for n > 2.
for n > 2.
Given a positive integer N, you are to write a program that computes two quantities regarding the solution of

where x, y, and z are constrained to be positive integers less than or equal to N. You are to compute the number of triples (x,y,z) such that x<y< z, and they are relatively prime, i.e., have no common divisor larger than 1. You are also to compute the number of values 0<p≤n such that p is not part of any triple (not just relatively prime triples).
This problem deals with computing quantities relating to part of Fermat's Last Theorem: that there are no integer solutions of
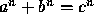 for n > 2.
for n > 2. Given a positive integer N, you are to write a program that computes two quantities regarding the solution of

where x, y, and z are constrained to be positive integers less than or equal to N. You are to compute the number of triples (x,y,z) such that x<y< z, and they are relatively prime, i.e., have no common divisor larger than 1. You are also to compute the number of values 0<p≤n such that p is not part of any triple (not just relatively prime triples).
输入解释
The input consists of a sequence of positive integers, one per line. Each integer in the input file will be less than or equal to 1,000,000. Input is terminated by end-of-file.
输出解释
For each integer N in the input file print two integers separated by a space. The first integer is the number of relatively prime triples (such that each component of the triple is <=N ). The second number is the number of positive integers <=N that are not part of any triple whose components are all <=N . There should be one output line for each input line.
输入样例
10 25 100
输出样例
1 4 4 9 16 27
来自杭电HDUOJ的附加信息
| Recommend | 8600 |
最后修改于 2020-10-25T22:46:29+00:00 由爬虫自动更新
共提交 249 次
通过率 51.0%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 65536/32768K(Java/Others) |
登陆或注册以提交代码