当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
1614:Stacking Boxes
题目描述
Some concepts in Mathematics and Computer Science are simple in one or two dimensions but become more complex when extended to arbitrary dimensions. Consider solving differential equations in several dimensions and analyzing the topology of an n-dimensional hypercube. The former is much more complicated than its one dimensional relative while the latter bears a remarkable resemblance to its ``lower-class'' cousin.
Consider an n-dimensional ``box'' given by its dimensions. In two dimensions the box (2,3) might represent a box with length 2 units and width 3 units. In three dimensions the box (4,8,9) can represent a box 4*8*9(length, width, and height). In 6 dimensions it is, perhaps, unclear what the box (4,5,6,7,8,9) represents; but we can analyze properties of the box such as the sum of its dimensions.
In this problem you will analyze a property of a group of n-dimensional boxes. You are to determine the longest nesting string of boxes, that is a sequence of boxesb1,b2,..bk such bi,that each box nests in box b(i+1)( 1≤i<k) .
A box D = ( d1,d2,...dn ) nests in a box E = ( e1,e2,...en ) if there is some rearrangement of the di, such that when rearranged each dimension is less than the corresponding dimension in box E. This loosely corresponds to turning box D to see if it will fit in box E. However, since any rearrangement suffices, box D can be contorted, not just turned (see examples below).
For example, the box D = (2,6) nests in the box E = (7,3) since D can be rearranged as (6,2) so that each dimension is less than the corresponding dimension in E. The box D = (9,5,7,3) does NOT nest in the box E = (2,10,6,8) since no rearrangement of D results in a box that satisfies the nesting property, but F = (9,5,7,1) does nest in box E since F can be rearranged as (1,9,5,7) which nests in E.
Formally, we define nesting as follows: box D = (d1,d2,....dn ) nests in box E = ( e1,e2,....en ) if there is a permutation π of 1..n such that (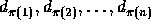 ) ``fits'' in ( e1,e2.....en ) i.e., if for all 1≤i≤n.
) ``fits'' in ( e1,e2.....en ) i.e., if for all 1≤i≤n.
Consider an n-dimensional ``box'' given by its dimensions. In two dimensions the box (2,3) might represent a box with length 2 units and width 3 units. In three dimensions the box (4,8,9) can represent a box 4*8*9(length, width, and height). In 6 dimensions it is, perhaps, unclear what the box (4,5,6,7,8,9) represents; but we can analyze properties of the box such as the sum of its dimensions.
In this problem you will analyze a property of a group of n-dimensional boxes. You are to determine the longest nesting string of boxes, that is a sequence of boxesb1,b2,..bk such bi,that each box nests in box b(i+1)( 1≤i<k) .
A box D = ( d1,d2,...dn ) nests in a box E = ( e1,e2,...en ) if there is some rearrangement of the di, such that when rearranged each dimension is less than the corresponding dimension in box E. This loosely corresponds to turning box D to see if it will fit in box E. However, since any rearrangement suffices, box D can be contorted, not just turned (see examples below).
For example, the box D = (2,6) nests in the box E = (7,3) since D can be rearranged as (6,2) so that each dimension is less than the corresponding dimension in E. The box D = (9,5,7,3) does NOT nest in the box E = (2,10,6,8) since no rearrangement of D results in a box that satisfies the nesting property, but F = (9,5,7,1) does nest in box E since F can be rearranged as (1,9,5,7) which nests in E.
Formally, we define nesting as follows: box D = (d1,d2,....dn ) nests in box E = ( e1,e2,....en ) if there is a permutation π of 1..n such that (
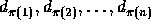 ) ``fits'' in ( e1,e2.....en ) i.e., if for all 1≤i≤n.
) ``fits'' in ( e1,e2.....en ) i.e., if for all 1≤i≤n. 输入解释
The input consists of a series of box sequences. Each box sequence begins with a line consisting of the the number of boxes k in the sequence followed by the dimensionality of the boxes, n (on the same line.)
This line is followed by k lines, one line per box with the n measurements of each box on one line separated by one or more spaces. The i(th) line in the sequence ( 1<=i<=k ) gives the measurements for i(th) the box.
There may be several box sequences in the input file. Your program should process all of them and determine, for each sequence, which of the k boxes determine the longest nesting string and the length of that nesting string (the number of boxes in the string).
In this problem the maximum dimensionality is 10 and the minimum dimensionality is 1. The maximum number of boxes in a sequence is 30.
This line is followed by k lines, one line per box with the n measurements of each box on one line separated by one or more spaces. The i(th) line in the sequence ( 1<=i<=k ) gives the measurements for i(th) the box.
There may be several box sequences in the input file. Your program should process all of them and determine, for each sequence, which of the k boxes determine the longest nesting string and the length of that nesting string (the number of boxes in the string).
In this problem the maximum dimensionality is 10 and the minimum dimensionality is 1. The maximum number of boxes in a sequence is 30.
输出解释
For each box sequence in the input file, output the length of the longest nesting string on one line followed on the next line by a list of the boxes that comprise this string in order. The ``smallest'' or ``innermost'' box of the nesting string should be listed first, the next box (if there is one) should be listed second, etc.
The boxes should be numbered according to the order in which they appeared in the input file (first box is box 1, etc.).
If there is more than one longest nesting string then any one of them can be output.
The boxes should be numbered according to the order in which they appeared in the input file (first box is box 1, etc.).
If there is more than one longest nesting string then any one of them can be output.
输入样例
5 2 3 7 8 10 5 2 9 11 21 18 8 6 5 2 20 1 30 10 23 15 7 9 11 3 40 50 34 24 14 4 9 10 11 12 13 14 31 4 18 8 27 17 44 32 13 19 41 19 1 2 3 4 5 6 80 37 47 18 21 9
输出样例
5 3 1 2 4 5 4 7 2 5 6
来自杭电HDUOJ的附加信息
| Recommend | 8600 |
最后修改于 2020-10-25T22:46:29+00:00 由爬虫自动更新
共提交 99 次
通过率 52.53%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 65536/32768K(Java/Others) |
登陆或注册以提交代码