当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
1485:Construct the wall maze
题目描述
In this problem you have to construct a maze using a maze construction kit consisting of:
1.a 6 by 6 grid of unit squares
2.3 walls of length between 1 and 6 which are placed either horizontally or vertically to separate squares
3.one start and one end marker
A maze may look like this:
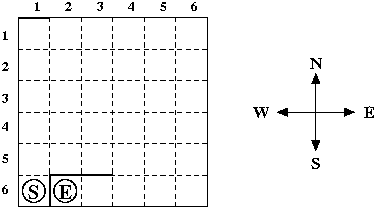
When a maze is finished, a shortest path between the square with the start marker and the square with the end marker is determined. Only moves between adjacent grid squares are allowed; adjacent means that the grid squares share an edge and are not separated by a wall. It is not allowed to leave the grid.
Your task is: given a shortest path of some maze, construct this maze. Obviously, the maze you construct should be valid, i.e., all 3 walls should be used, they should not intersect with each other (although they may touch at some grid corner), and the walls should not stick out of the grid. Moreover, the given path should be valid for this maze, i.e., it should lead from the square with the start marker to the square with the end marker without crossing any wall or going outside of the grid, and there shouldn't exist any shorter valid path.
1.a 6 by 6 grid of unit squares
2.3 walls of length between 1 and 6 which are placed either horizontally or vertically to separate squares
3.one start and one end marker
A maze may look like this:

When a maze is finished, a shortest path between the square with the start marker and the square with the end marker is determined. Only moves between adjacent grid squares are allowed; adjacent means that the grid squares share an edge and are not separated by a wall. It is not allowed to leave the grid.
Your task is: given a shortest path of some maze, construct this maze. Obviously, the maze you construct should be valid, i.e., all 3 walls should be used, they should not intersect with each other (although they may touch at some grid corner), and the walls should not stick out of the grid. Moreover, the given path should be valid for this maze, i.e., it should lead from the square with the start marker to the square with the end marker without crossing any wall or going outside of the grid, and there shouldn't exist any shorter valid path.
输入解释
The input consists of several test cases. Every test case starts with a line containing three positive integers, the length of the three walls of the maze construction kit. The next line consists of 1 to 25 characters from the set {'N', 'E', 'S', 'W'} and describes a shortest path from the start to the end marker in the maze to be constructed. Each character specifies the direction of the next move (see picture). You may assume that each test case has at least one solution.
The last test case is followed by a line containing three zeros.
The last test case is followed by a line containing three zeros.
输出解释
For each test case produce five lines of output: First the column and row number of the square containing the start marker, then the column and row number of the square containing the end marker, then the location of the three walls (in the same order as the given lengths in the input). The location of a wall should be specified by either the position of its left end point followed by the position of its right end point (in case of a horizontal wall) or the position of its upper end point followed by the position of its lower end point (in case of a vertical wall). The position of a wall end point should be given as the distance from the left side of the grid followed by the distance from the upper side of the grid.
There can be several valid solutions for a given test case (for example the test case in the sample input). Your program may print any of those solutions. Note that the sample output specifies the maze from the picture above.
There can be several valid solutions for a given test case (for example the test case in the sample input). Your program may print any of those solutions. Note that the sample output specifies the maze from the picture above.
输入样例
1 1 2 NEEESWW 0 0 0
输出样例
1 6 2 6 0 0 1 0 1 5 1 6 1 5 3 5
来自杭电HDUOJ的附加信息
| Recommend | JGShining |
最后修改于 2020-10-25T22:45:22+00:00 由爬虫自动更新
共提交 112 次
通过率 65.18%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 65536/32768K(Java/Others) |
登陆或注册以提交代码