当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
1476:Scheduling Lectures
题目描述
You are teaching a course and must cover n (1 <= n <= 1000) topics. The length of each lecture is L (1 <= L <= 500) minutes. The topics require t1, t2, ..., tn (1 <= ti <= L) minutes each. For each topic, you must decide in which lecture it should be covered. There are two scheduling restrictions:
1. Each topic must be covered in a single lecture. It cannot be divided into two lectures. This reduces discontinuity between lectures.
2. Topic i must be covered before topic i + 1 for all 1 <= i < n. Otherwise, students may not have the prerequisites to understand topic i + 1.
With the above restrictions, it is sometimes necessary to have free time at the end of a lecture. If the amount of free time is at most 10 minutes, the students will be happy to leave early. However, if the amount of free time is more, they would feel that their tuition fees are wasted. Therefore, we will model the dissatisfaction index (DI) of a lecture by the formula:
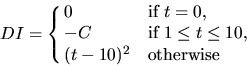
where C is a positive integer, and t is the amount of free time at the end of a lecture. The total dissatisfaction index is the sum of the DI for each lecture.
For this problem, you must find the minimum number of lectures that is needed to satisfy the above constraints. If there are multiple lecture schedules with the minimum number of lectures, also minimize the total dissatisfaction index.
This problem contains multiple test cases!
The first line of a multiple input is an integer N, then a blank line followed by N input blocks. Each input block is in the format indicated in the problem description. There is a blank line between input blocks.
The output format consists of N output blocks. There is a blank line between output blocks.
1. Each topic must be covered in a single lecture. It cannot be divided into two lectures. This reduces discontinuity between lectures.
2. Topic i must be covered before topic i + 1 for all 1 <= i < n. Otherwise, students may not have the prerequisites to understand topic i + 1.
With the above restrictions, it is sometimes necessary to have free time at the end of a lecture. If the amount of free time is at most 10 minutes, the students will be happy to leave early. However, if the amount of free time is more, they would feel that their tuition fees are wasted. Therefore, we will model the dissatisfaction index (DI) of a lecture by the formula:
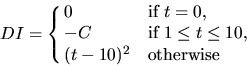
where C is a positive integer, and t is the amount of free time at the end of a lecture. The total dissatisfaction index is the sum of the DI for each lecture.
For this problem, you must find the minimum number of lectures that is needed to satisfy the above constraints. If there are multiple lecture schedules with the minimum number of lectures, also minimize the total dissatisfaction index.
This problem contains multiple test cases!
The first line of a multiple input is an integer N, then a blank line followed by N input blocks. Each input block is in the format indicated in the problem description. There is a blank line between input blocks.
The output format consists of N output blocks. There is a blank line between output blocks.
输入解释
The input consists of a number of cases. The first line of each case contains the integer n, or 0 if there are no more cases. The next line contains the integers L and C. These are followed by n integers t1, t2, ..., tn.
输出解释
For each case, print the case number, the minimum number of lectures used, and the total dissatisfaction index for the corresponding lecture schedule on three separate lines. Output a blank line between cases.
输入样例
6 30 15 10 10 10 10 10 10 10 120 10 80 80 10 50 30 20 40 30 120 100 0
输出样例
Case 1: Minimum number of lectures: 2 Total dissatisfaction index: 0 Case 2: Minimum number of lectures: 6 Total dissatisfaction index: 2700
来自杭电HDUOJ的附加信息
| Recommend | lcy |
最后修改于 2020-10-25T22:45:18+00:00 由爬虫自动更新
共提交 8 次
通过率 12.5%
| 时间上限 | 内存上限 |
| 20000/10000MS(Java/Others) | 65536/32768K(Java/Others) |
登陆或注册以提交代码