当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
1246:自共轭Ferrers图
题目描述
Ferrers图是一个自上而下的n层格子,且上层格子数不少于下层格子数。
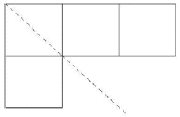
如上图所示,图中的虚线称为Ferrers图的虚轴。若将图一绕虚轴旋转180°,即将第一行与第一列对调,将第二行与第二列对调,……,这样所得到的图仍为Ferrers图,如下图所示。
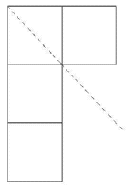
这两个图称为一对共轭Ferrers图。有一些Ferrers图,沿虚轴转换后的Ferrers图仍为它本身,也就是说这个Ferrers图关于虚轴对称,那么这个Ferrers图称为自共轭Ferrers图。下图便是一个自共轭Ferrers图。
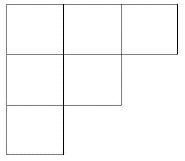
现在我们的目标是寻找的是大小为n的自共轭Ferrers图的总数。所谓大小为n的自共轭Ferrers图是指由n个方格组成的自共轭Ferrers图。

如上图所示,图中的虚线称为Ferrers图的虚轴。若将图一绕虚轴旋转180°,即将第一行与第一列对调,将第二行与第二列对调,……,这样所得到的图仍为Ferrers图,如下图所示。

这两个图称为一对共轭Ferrers图。有一些Ferrers图,沿虚轴转换后的Ferrers图仍为它本身,也就是说这个Ferrers图关于虚轴对称,那么这个Ferrers图称为自共轭Ferrers图。下图便是一个自共轭Ferrers图。

现在我们的目标是寻找的是大小为n的自共轭Ferrers图的总数。所谓大小为n的自共轭Ferrers图是指由n个方格组成的自共轭Ferrers图。
输入解释
输入数据有多行,每行为一个正整数n(1<=n<=300)。表示自共轭Ferrers图的大小为n。
输出解释
对应输入的每一个n,输出一行大小为n的自共轭Ferrers图的总数。
输入样例
1 2 3
输出样例
1 0 1
来自杭电HDUOJ的附加信息
| Author | weigang Lee |
| Recommend | Ignatius.L |
最后修改于 2020-10-25T22:43:14+00:00 由爬虫自动更新
共提交 16 次
通过率 25.0%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 65536/32768K(Java/Others) |
登陆或注册以提交代码